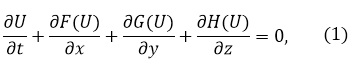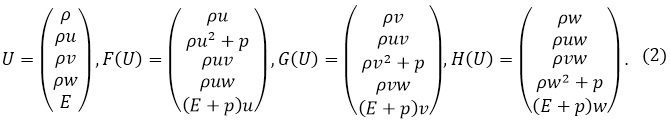аспирант, кафедра прикладной математики, дифференциальных уравнений и теоретической механики, факультет математики и информационных технологий, Федеральное государственное бюджетное образовательное учреждение высшего образования «Мордовский государственный университет им. Н.П. Огарёва»
Математическое моделирование физических процессов в областях со сложными геометриями является достаточно трудоемким процессом, как с точки зрения программной реализации методик, так и с точки зрения календарного времени решения задачи. Конечной целью любого моделирования является технология подготовки и проведения расчета в разумные календарные сроки. Подготовку к решению задачи можно разбить на несколько этапов:
1) подготовка сеточной модели;
2) математическая постановка задачи (выбор модели, задание начальных параметров, параметров граничных условий, параметров счета и других параметров);
3) собственно проведение расчета.
В данной работе предлагается кратко рассмотреть три вида сеточных моделей: структурированные сетки, неструктурированные и адаптивно-встраиваемые.
- Структурированные сетки
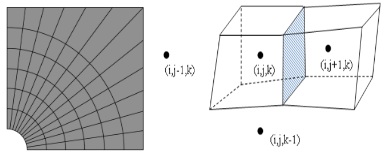
Структурированная сетка – это сетка, у которой множество сеточных узлов является упорядоченным (рис. 1).
Рис.1. Ячейки структурированной сетки
Использование структурированных сеток (по сравнению с неструктурированными) позволяет, как правило, уменьшить продолжительность расчета и необходимый объём оперативной памяти [2]. Структура данных регулярной сетки подразумевает хранение следующих элементов:
- количество ячеек по криволинейным координатным направлениям I, J, K.
- глобальный номер ячейки; глобальную нумерацию можно определить, последовательно пронумеровав ячейки сначала по направлению i, затем по j и далее по k;
- ячеечный массив, соответствующий значению физической величины в центре ячейки, представляет собой линейный массив размерности N; N = I*J*K;
- глобальный номер грани; нумерация граней вводится, также как и нумерация ячеек, последовательной нумерацией по координатным направлениям, при этом сначала нумеруются грани по первому координатному направлению, затем по второму и далее по третьему;
- граневый массив, соответствующий значению физической величины в центре грани, представляет собой линейный массив размерности 3M, М=(I+1)×(J+1)×(K+1).
- Неструктурированные сетки
Неструктурированные сетки – сетки с произвольным расположением узлов. Состоят такие сетки из ячеек различной формы (преимущественно шестигранники или тетраэдры). Они могут быть сформированы и объединены грань в грань произвольным образом для заполнения любого объёма, например системы охлаждения двигателя (рис. 2).
Рис. 2. Сетка системы охлаждения двигателя
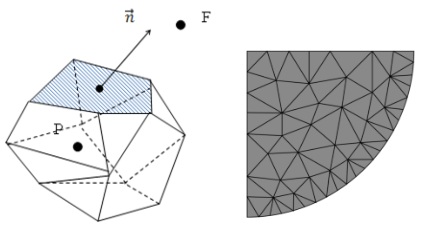
Обычно грани таких ячеек – произвольные многоугольники (рис. 3).
Рис. 3. Пример ячеек неструктурированной сетки
Для хранения информации о структуре сетки используют следующие элементы:
- количество узлов NV; количество граней NF; количество ячеек NC;
- номер узла v, v = 1, NV;
- узловой массив, соответствующий значению физической величины в узле ячейки, представляет собой линейный массив размерности NV; первый элемент данного массива соответствует значению в узле с номером 1, второй – 2 и так далее;
- структура узлов сетки содержит: три узловых массива координат узлов, глобальный массив номеров ячеек, отсортированный по номеру узла, узловой массив количества ячеек, имеющих текущий узел;
- номер грани f, f = 1, NF;
- граневый массив, соответствующий значению физической величины в центре грани, представляет собой линейный массив размерности NF;
- структура граней содержит: граневые массивы номеров ячеек 1 и 2 (предполагается, что нормаль, отнесенная к центру грани, направлена из ячейки 1 в ячейку 2); глобальный массив номеров узлов, отсортированных по номеру грани, граневый массив количества узлов; граневый массив смещений в массиве глобальных номеров узлов;
- номер ячейки c , с = 1, NC;
- ячеечный массив, соответствующий значению физической величине в центре ячейки, представляет собой линейный массив размерности NC;
- структура ячеек содержит: глобальный массив номеров граней, отсортированных по номеру ячейки, ячеечный массив количества граней, ячеечный массив смещений в массиве глобальных номеров граней.
- Адаптивные сетки
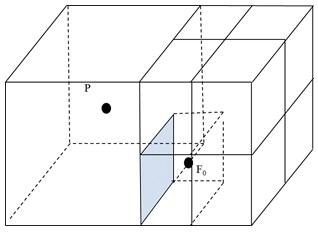
Адаптивные сетки – сетки, перестраивающиеся в процессе расчета [1]. После построения базовой сетки производится ее дробление на равные подобные ячейки (в трехмерном случае на 8 ячеек), при этом предполагается, что ячейка через грань не может иметь больше четырех соседей. На рисунке 4 показан пример ячейки адаптивно-встраиваемой сетки. Адаптация или дробление расчетной сетки осуществляется по заданным критериям: возможно проведение адаптации к поверхности расчетной области или в выделенном геометрическом объеме.
Рис. 4. Пример ячейки адаптивно-встраиваемой сетки
Адаптация расчетной сетки в описанной сеточной модели, является одним из трудоемких и сложных в реализации. Хранение данных в первую очередь подразумевает достаточно гибкие и удобные алгоритмы по добавлению и удалению ячеек, как при проведении адаптации, так и при изменении геометрии.
Оптимальным для хранения данной сеточной модели является дерево ячеек, на верхнем уровне которого расположены ячейки базовой сетки, имеющие регулярные интерфейсы работы с ними. Адаптивные ячейки являются дочерними, при этом на каждом уровне дерева сохраняются виртуальные объекты, которые определяют либо признак дробления сетки, либо отсечения геометрией. Для каждого элемента дерева (ячейки) хранятся: данные, списки граней и другая вспомогательная информация. Так как на описанной сетке предполагается реализация конечно-объемных методов, то в структурах хранения данных не сохраняются координаты вершин, а только площади и центры граней, объемы и центры расчетных ячеек и данные о связности ячеек.
Определение. Задача построения расчетной сетки заключается в нахождении отображения, которое переводит узлы сетки из физической области (D) в вычислительную область (CD). Отображение должно удовлетворять некоторым требованиям.
1) оно должно быть однозначным;
2) линии сетки должны быть гладкими, что обеспечивает непрерывность производных;
3) сетка должна быть достаточно густой в тех частях области D, где ожидается возникновение больших численных ошибок;
4) следует избегать излишней скошенности ячеек, которая иногда приводит к чрезмерной ошибке аппроксимации.
- Пример расчета на адаптивной сетке
В качестве примера использования расчетных сеток рассмотрим решение задачи о движении ударной волны в трубе с элегазом (SF6) на адаптивной сетке [3].
Постановка задача была следующая: ударная волна проходит через тонкую мембрану, разделяющую элегаз и воздух, находящиеся при атмосферном давлении. Физические параметры следующие: начальная температура 291 K, давление 0,1 МПа = 1 бар. За ударной волной в элегазе давление 2.152 бар, плотность 1.209*10-2г/см3, скорость ударной волны 195.2 м/c, скорость течения за ударной волной 97.76 м/с, начальные плотности элегаза и воздуха в камере низкого давления 6.037*10-3 и 1.198*10-3 г/см3 соответственно. Физические свойства элегаза и воздуха следующие: оба вещества являются невязкими, нетеплопроводными и идеальными газами с показателями адиабаты γ=1,094(SF6) и γ=1,4(воздух). Отношение молекулярных масс (SF6/воздух) принято равным 5.04.
Целью расчетов было получение и анализ временных зависимостей пульсаций продольной компоненты скорости 〈w2〉 — 〈w〉2.
Для описания исследуемых процессов использовалась модель невязкого, нетеплопроводящего идеального газа, описываемая системой уравнений Эйлера:
где
Система замыкается уравнением состояния p = (γ-1)ερ. B (2)
![]()
ρ – плотность, u,v,w – компоненты вектора скорости V,ε – удельная внутренняя энергия на единицу объема, p – давление, γ – показатель адиабаты.
Было принято, что положение контактного разрыва соответствует значению продольной координаты z=0, воздух низкого давления занимает первоначально промежуток 0≤z≤300 мм. Координаты датчиков имеют следующие значения: 1-й датчик − z = 51 мм, 2-й датчик − z = 125.5 мм, 3-й датчик − z = 161 мм, 4-й-датчик − z = 169 мм, 5-й датчик − z = 178.5 мм. Начальные условия задаются следующим образом. В области zmin≤z≤zSW<0 задано состояние элегаза за ударной волной с числом Маха 1.45, в области zSW<z<0 − состояние покоящегося элегаза при атмосферном давлении, в области 0≤z≤300 мм − состояние покоящегося воздуха при атмосферном давлении. Во всех расчетах принято zSW = −5 мм, чтобы время достижения ударной волны контактного разрыва было мало по сравнению со всем временем расчета (2000 мкс).
На рисунках ниже представлено моделирование плотности газов на границе раздела сред. На них показывается, как адаптивная сетка сгущается с течением времени в областях больших градиентов плотности (рис. 5–9). На рисунках показано начальное состояние и первые 4 итерации расчёта.
Рис. 5. Адаптивная сетка. Итерация 0
На рис. 5 самая светлая область на левом изображении – это плотность воздуха за ударной волной, равная 1.209*10-2г/см3. Самая темная область – плотность воздуха в камере низкого давления, равная 1.198*10-3 г/см3. Прослойка между этими двумя областями – область, где находится SF6 с плотностью 6.037*10-3 г/см3. Справа изображена соответствующая сетка.
Рис. 6. Адаптивная сетка. Итерация 1
Рис. 7. Адаптивная сетка. Итерация 2
Рис. 8. Адаптивная сетка. Итерация 3
Рис. 9. Адаптивная сетка. Итерация 4
Список использованных источников
- Андерсон Д., Таннехилл Дж., Плетчер Р. Вычислительная гидромеханика и теплообмен. В 2-х т. Т. 2 / Пер. с англ. М.: Мир, 1990. С.728–392 с.
- Флетчер К. Вычислительные методы в динамике жидкостей: В 2-х т. Т. 2 / Пер. с англ. М.: Мир, 1991. 552 c.
- Жалнин Р. В., Змитренко Н. В., Ладонкина М. Е., Тишкин В. Ф. Численное моделирование развития неустойчивости Рихтмайера-Мешкова с использованием схем высокого порядка точности // Математическое моделирование. 2007. Т. 19, № 10. С. 61–66.
Mavrin Aleksey
postgraduate student, Department of Applied Mathematics, Differential Equations and Theoretical Mechanics, Faculty of Mathematics and Information Technologies, Federal State Budgetary Educational Institution of Higher Education «National Research Ogarev Mordovia State University»
TYPES OF CALCULATING GRIDS AND METHODS FOR INFORMATION STORAGE ABOUT THEM
The paper reviews the main types of calculating grids and methods for information storing about the structure of such grids. The article gives examples of all three types of calculating grids and solves the problem of the shock wave motion calculating using an adaptive grid.
Keywords: physical area, calculating area, regular grids, non-structured grids, adaptive grids.
© АНО СНОЛД «Партнёр», 2018
© Маврин А. С., 2018