Узлы и элементы, сгенерированные в моделях, составляют сетку конечных элементов. Определяются контактные взаимодействия. Задаются закрепления и нагружения моделей, максимально приближенные к физически проведенным экспериментам. Для определения усталостной прочности деталей соединения к проекту подключается модуль расчета усталостной прочности.
Разработанные конечно-элементные модели соединений могут использоваться с целью определения характеристик и усталостной прочности при поверочном расчете вновь создаваемых соединений и уточнении ресурса используемых.
магистрант, направление «Технология машиностроения», Арзамасский Политехнический Институт (филиал Нижегородского государственного технического университета им. Р. Е. Алексеева), г. Арзамас
Ломакин Сергей Николаевич
магистрант, направление «Технология машиностроения», Арзамасский Политехнический Институт (филиал Нижегородского государственного технического университета им. Р. Е. Алексеева), г. Арзамас
Гришин Александр Иванович
магистрант, направление «Технология машиностроения», Арзамасский Политехнический Институт (филиал Нижегородского государственного технического университета им. Р. Е. Алексеева), г. Арзамас
Шурыгин Алексей Юрьевич
кандидат технических наук, доцент, кафедра «Технология машиностроения», Арзамасский Политехнический Институт (филиал Нижегородского государственного технического университета им. Р. Е. Алексеева), г. Арзамас
Проектирование и расчет различных типов соединенийдеталей машин производится в соответствии с указаниями, изложенными в нормативных документах и в специальной литературе по деталям машин. При этом назначаются размеры деталей соединений в зависимости от предполагаемых условий нагружения.Неравномерность распределения нагрузок оказывает существенное влияние на работоспособность соединений и не учитывается в расчетах. Это показывает, что для уточненного расчета деталей соединений следует использовать современные методы численного моделирования с использованием систем конечно-элементного анализа.
Объектом исследования являются геометрические модели деталей шлицевого и клинового соединений, имеющих формат 3D (*.stp) которые импортированы в расчетную систему ANSYS®Mechanical для проведения статического анализа. Деталям исследуемых моделей определены свойства конструкционной стали 40X: плотность – 7,85∙10-6kg mm-3; модуль Юнга – 2∙10 МПА; коэффициент Пуассона – 0,3.
Узлы и элементы, сгенерированные в моделях, в совокупности составляют сетку конечных элементов. Для создания конечно-элементных моделей, шлицевого и клинового соединений, использованы следующие типы конечных элементов: Tet10, Hex20, Wed15, Pyr13.В качестве метода создания конечно-элементных моделей на телах принимается Multi Zone.
Определение контактных поверхностей и современные алгоритмы позволяют быстро и точно смоделировать взаимодействие [1]. Для моделирования контактного взаимодействия множества деталей исследуемых моделейиспользован контакт без разделения (NoSeparation)– для моделирования скользящих беззазорных соединений, например, осей во втулках, направляющих и т.п. Скольжение в контакте ничем не ограничено, зазор не допускается.
Правильное задание закрепления и нагружения моделей позволяет получить результаты, максимально приближенные к физически проведенным экспериментам [2]. Для моделирования закрепления и нагружений деталей в конструкциях шлицевого и клинового соединений использованы приведенные ниже типы нагрузок и граничных условий.
Для моделирования закрепления использовано граничное условие – «Fixed Support» ограничивающая для указанных поверхностей степени свободы x, y, z, rotx, roty и rotz.
Для исследования характера изменения напряженного состояния деталей шлицевого соединения при приложении рабочей нагрузки к зубчатому колесу прикладывается момент величиной 200 Нм.
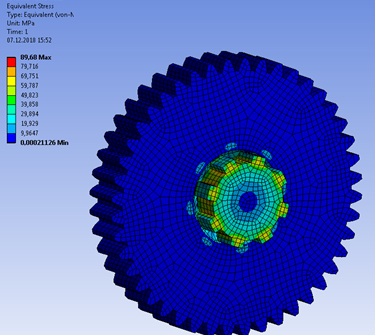
Анализ результатов исследования (рисунок1) показывает, что в деталях шлицевого соединения, возникают значительные напряжения, неравномерные по длине контактирующих поверхностей деталей соединения, что не учитывается при выполнении их проверочных расчетов по формулам сопротивления материалов.
Рис.1. Рассчитанные эпюры напряжений, возникающие в деталях шлицевого соединения при приложении момента 200Нм
Для исследования характера изменения напряженного состояния деталей шлицевого соединения, при приложении рабочего диапазона нагрузок, с использованием программного комплекса ANSYS®Mechanical разработанная выше конечно-элементная модель исследуется со следующими параметрами: рабочие моменты изменяются в диапазоне от 200 до 1300 Нм.
Результаты исследования напряжений в деталях шлицевого соединения «Колесо» и «Вал» при изменении момента от 200Нм до 1300Нм приведены в таблице1.
Таблица 1.
Напряжение в деталях шлицевого соединения при изменении момента от 200Нм до 1300Нм
| Момент нагрузки, Нм | 200 | 300 | 500 | 900 | 1100 | 1300 |
| Напряжения на детали «Зубчатое колесо», МПа | 57 | 84 | 141 | 255 | 311 | 368 |
| Напряжения на детали «Вал шлицевой», МПа | 89 | 134 | 224 | 403 | 493 | 582 |
На рисунке 2 приведены график зависимости напряжений в деталях шлицевого соединения при изменении момента от 200Нм до 1300Нм.
Рис.2. График зависимости коэффициентов запаса прочности деталей шлицевого соединения при изменении момента нагрузки
Рассчитанные коэффициенты запаса прочности деталей шлицевого соединения в зависимости от момента нагрузки от 200Нм до 1300Нм приведены вна рисунке 3.
Рис. 3. График зависимости коэффициентов запаса прочности деталей шлицевого соединения при изменении момента от 200Нм до 1300Нм
Полученные графики зависимостей напряжений и коэффициентов запаса прочности деталей шлицевого соединения при изменении момента нагрузки следует использовать при поверочном расчете вновь создаваемых соединений и уточнении ресурса используемых.
Для рассматриваемой конструкции шлицевого соединения при заданных внешних воздействиях получено решение статической задачи. Для определения усталостной прочности деталей шлицевого соединения к проекту подключается модульрасчета усталостной прочности.
Рассчитанные эпюры распределения параметра «Stress Life» при приложении нагрузки в виде момента величиной 200 Нм приведены на рисунке 4.
Рис. 4. Рассчитанные эпюры распределения параметра «StressLife» при приложении нагрузки в виде момента величиной 200 Нм
Для исследования усталостной прочности деталей шлицевого соединения, при приложении рабочего диапазона нагрузок, с использованием программного комплекса ANSYS®Mechanical разработанная выше конечно-элементная модель исследуется со следующими параметрами: рабочие моменты изменяются в диапазоне от 200 до 1300 Нм.
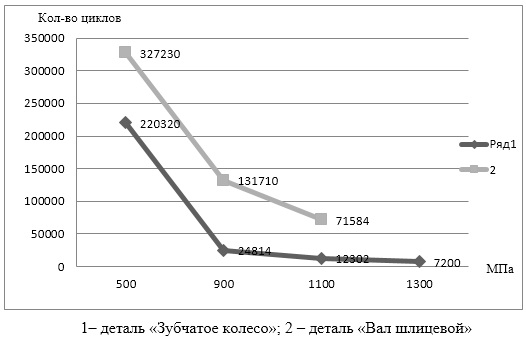
Результаты исследования количества циклов нагружения, выдерживаемых шлицевым валом и зубчатым колесом (параметр «StressLife») при изменении момента от 200Нм до 1300Нм, приведены в таблице 2.
Таблица 2.
Количество циклов нагружения, выдерживаемых деталями шлицевого соединения при изменении момента от 200Нм до 1300Нм
| Момент нагрузки, Нм | 200 | 300 | 500 | 900 | 1100 | 1300 |
| Количество циклов детали «Вал шлицевой», шт | >1млн | >1млн | 220320 | 24814 | 12302 | 7200 |
| Количество циклов детали «Зубчатое колесо», шт | >1млн | >1млн | >1млн | 327230 | 131710 | 71584 |
На рисунке 5 приведен график зависимостей количества циклов нагружения, выдерживаемых деталями шлицевого соединения (параметр «StressLife») при изменении момента от 200Нм до 1300Нм.
Рис.5. График зависимостей количества выдерживаемых циклов деталями шлицевого соединения при изменении момента нагрузки
Полученные графики зависимостей количества циклов нагружения, выдерживаемых деталями шлицевого соединения при изменении момента нагрузки, следует использовать при поверочном расчете вновь создаваемых шлицевых соединений и уточнении ресурса используемых.
Разработанные конечно-элементные модели шлицевых соединений с целью определения прочностных характеристик и усталостной прочности могут использоваться при поверочном расчете вновь создаваемых соединений и уточнении ресурса используемых.
Для исследования характера изменения напряженного состояния деталей клинового соединения при приложении тяговой силы в диапазоне от 500кН до 1000кН к хвостовику протяжки прикладывается граничное условие Force.
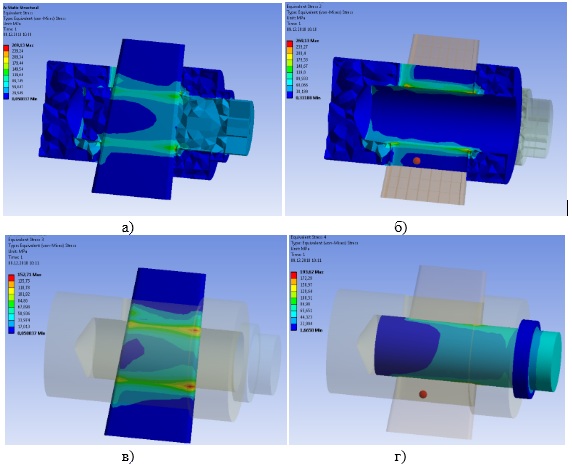
Анализ результатов исследования (рисунок6) показывает, что в деталях клинового соединения, возникают значительные напряжения, неравномерные по длине контактирующих поверхностей деталей соединения, что не учитывается при выполнении их проверочных расчетов по формулам сопротивления материалов.
Рис.6. Эпюры напряжений, возникающие в деталях (а) клинового соединения: «Втулка»(б),
«Клин» (в), «Хвостовик» (г)
Для исследования характера изменения напряженного состояния деталей клинового соединения, при приложении рабочего диапазона нагрузок, с использованием программного комплекса ANSYS®Mechanical разработанная выше конечно-элементная модель исследуется со следующими параметрами: тяговая сила изменяется в диапазоне от 500кН до 1000кН.
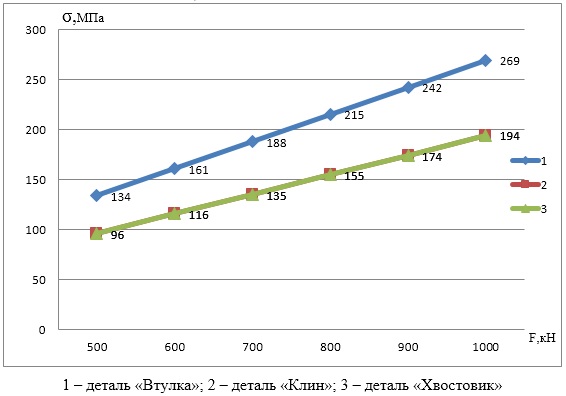
Результаты исследования напряжений деталей «Втулка», «Клин» и «Хвостовик» при изменении тяговой силы от 500кН до 1000кН и соответствующие коэффициенты запаса прочности приведены в таблицах 3 и 4.
Таблица 3.
Напряжения в деталях клинового соединения при изменении тяговой силы от 500кН до 1000кН
| Тяговая сила, кН | 500 | 600 | 700 | 800 | 900 | 1000 |
| Напряжения в детали «Втулка», МПа | 134 | 161 | 188 | 215 | 242 | 269 |
| Напряжения в детали «Клин», МПа | 76 | 92 | 106 | 122 | 137 | 153 |
| Напряжения в детали «Хвостовик», МПа | 96 | 116 | 135 | 155 | 174 | 194 |
На рисунках 7 и 8 приведены графики зависимости напряжений и коэффициентов запаса прочности деталей «Втулка», «Клин» и «Хвостовик» при изменении тяговой силы от 500кН до 1000кН.
Коэффициент запаса – величина, показывающая способность конструкции выдерживать прилагаемые к ней нагрузки выше расчётных. Наличие запаса прочности обеспечивает дополнительную надёжность конструкции, чтобы избежать катастрофы в случае возможных ошибок проектирования, изготовления или эксплуатации.
Рис.7. График зависимости напряжений в деталях «Втулка», «Клин» и «Хвостовик» при изменении тяговой силы от 500кН до 1000кН
Таблица 4.
Коэффициент запаса прочности деталей «Втулка», «Клин» и «Хвостовик» при изменении тяговой силы от 500кН до 1000кН
| Момент нагрузки, кН | 500 | 600 | 700 | 800 | 900 | 1000 |
| Коэффициент запаса прочности детали «Втулка» | 4,9 | 4,0 | 3,5 | 3,0 | 2,7 | 2,4 |
| Коэффициент запаса прочности детали «Клин» | 8,6 | 7,1 | 6,1 | 5,3 | 4,7 | 4,2 |
| Коэффициент запасапрочности детали «Хвостовик» | 6,8 | 5,6 | 4,8 | 4,2 | 3,7 | 3,4 |
Полученные графики зависимостей напряжений и коэффициентов запаса прочности деталей клинового соединения при изменении тяговой силы следует использовать при поверочном расчете вновь создаваемых соединений и уточнении ресурса используемых.
Для рассматриваемой конструкции клинового соединения с учетом внешних воздействий получено решение статической задачи, после чего добавляется модуль расчета усталостной прочности.
Рис.8. График зависимости коэффициентов запаса прочности деталей «Втулка», «Клин» и «Хвостовик» при изменении тяговой силы
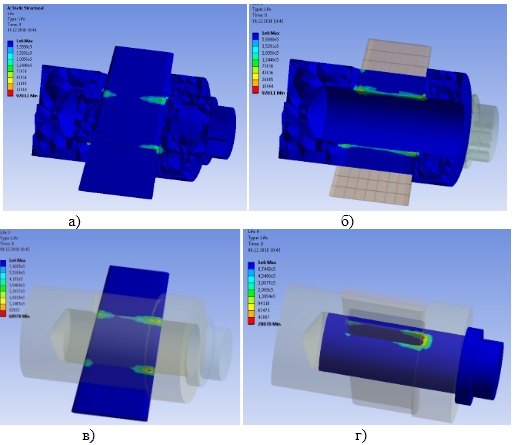
Эпюры распределения параметра «Life», возникающие в деталях клинового соединения, приведены на рисунке 9.
Рис.9.Эпюры распределения параметра «Life» возникающие в деталях (а) клинового соединения: «Втулка»(б), «Клин» (в) «Хвостовик» (г)
Для исследования усталостной прочности деталей клинового соединения, при приложении рабочего диапазона нагрузок, с использованием программного комплекса ANSYS®Mechanical разработанная выше конечно-элементная модель исследуется со следующими параметрами: тяговые силы изменяются в диапазоне от 500кН до 1000кН.
Результаты исследования количества циклов, выдерживаемых деталями клинового соединения (параметр «StressLife») при изменении тяговой силы от 500кН до 1000кН, приведены в таблице 5.
Таблица 5.
Количество циклов, выдерживаемых деталями клинового соединения (параметр «StressLife») при изменении тяговой силы от 500кН до 1000кН
| Тяговая сила, кН | 500 | 600 | 700 | 800 | 900 | 1000 |
| Количество циклов детали «Втулка»,шт | 109570 | 56190 | 31920 | 19587 | 13085 | 9203 |
| Количество циклов детали «Клин», шт | 1000000 | 703720 | 289700 | 155610 | 101500 | 68970 |
| Количество циклов детали «Хвостовик», шт | 512510 | 186750 | 106750 | 65758 | 42492 | 28870 |
На рисунке 10 приведен график зависимости количества выдерживаемых циклов деталями клинового соединения (параметр «Stress Life») при изменении тяговой силы от 500кН до 1000кН.
Рис.10. График зависимости количества выдерживаемых циклов деталями клинового соединения (параметр «StressLife») при изменении тяговой силы от 500кН до 1000кН
Полученные графики зависимостей зависимости количества выдерживаемых циклов деталями клинового соединения (параметр «StressLife») при изменении тяговой силы от 500кН до 1000кН следует использовать при поверочном расчете вновь создаваемых клиновых соединений и уточнении ресурса используемых.
Список использованных источников
- Основы работы в ANSYS 17 / Н. Н. Федорова, С. А. Вальгер, М. Н. Данилов, Ю. В. Захарова. М.: ДМК Пресс, 2017. 210 с.
- Иванов Д.В., Доль А.В. Введение в AnsysWorkbench: учеб.-метод. пособие для студентов естественно-научных дисциплин. Саратов:Амирит, 2016. – 56 с.
Vanyukhin Sergey
student, Arzamas Polytechnic Institute (branch of R. E. Alekseev Nizhny Novgorod State Technical University), Arzamas
Lomakin Sergey
student, Arzamas Polytechnic Institute (branch of R. E. Alekseev Nizhny Novgorod State Technical University), Arzamas
Grishin Alexander
student, Arzamas Polytechnic Institute (branch of R. E. Alekseev Nizhny Novgorod State Technical University), Arzamas
Shurygin Alexey
Doctor of Technical Sciences, Associate Professor, Department Engineering Technology, Arzamas Polytechnic Institute (branch of R. E. Alekseev Nizhny Novgorod State Technical University), Arzamas
DEVELOPMENT AND RESEARCH OF FINITE ELEMENT MODELS OF DIFFERENT CONNECTION TYPES USING “ANSYS®MECHANICAL” TO DETERMINE THEIR STRENGTH AND FATIGUE STRENGTH CHARACTERISTICS
The article deals with the development and research of finite element models of various types of compounds using «ANSYS®MECHANICAL». The purpose of the research is to determine the strength characteristics and fatigue strength. 3D format (*.stp) compounds geometrical models are imported into ANSYS®Mechanical calculation system for static analysis. The material properties are assigned to the details of the studied models.
The nodes and elements that are generated in the models form a finite element grid. Contact interactions are defined. Fixing and loading of models which are as approximate close as possible to physically carried out experiments are set. To determine the connection parts fatigue strength, the calculation module is connected to the project.
The developed finite-element models of compounds can be used to determine the characteristics and fatigue strength in the verification calculation of newly created compounds and resource refinement of already used compounds.
Keywords: finite element model, ANSYS®Mechanical calculation system, fatigue strength calculation module.
© АНО СНОЛД «Партнёр», 2019
© Ванюхин С. М., 2019
© Ломакин С. Н., 2019
© Гришин А. И., 2019
© Шурыгин А. Ю., 2019